Basic Theory

This is only a brief overview of the Boys function. For more details, see

The Boys function is defined as

$F_m(t) = \int_0^1 u^{2m} e^{-tu^2} du \qquad \qquad t \ge 0$

and is related to the gamma function 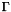$\Gamma$

$F_m(t) = \frac{e^{-t}}{2} \Gamma\left(m+\frac{1}{2}\right) \sum_{i=0}^{\infty} \frac{t^i}{\Gamma\left(m+i+\frac{3}{2}\right)}$

and to the lower incomplete gamma function 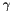$\gamma$

$F_m(t) = \frac{1}{2t^{m+\frac{1}{2}}} \gamma\left( m+\frac{1}{2}, t\right)$

The Boys function has the following downward and upward recurrence relations (respectively)

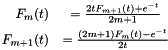
$\begin{eqnarray*} F_m(t) &= \frac{2t F_{m+1}(t) + e^{-t}}{2m+1} \\ F_{m+1}(t) &= \frac{(2m+1)F_m(t) - e^{-t}}{2t} \end{eqnarray*}$

It should be noted that under some conditions (small 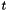$t$ ), upwards recurrence is numerically unstable.

Lastly, values for m=0 and for t=0 can be calculated easily

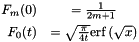
$\begin{eqnarray*} F_m(0) &= \frac{1}{2m+1} \\ F_0(t) &= \sqrt{\frac{\pi}{4t}}\mathrm{erf}\left(\sqrt{x}\right) \end{eqnarray*}$

In practice, due to the unbounded nature of 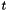$t$ , evaluation is usually split into three regimes

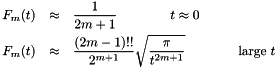
$\begin{eqnarray*} F_m(t) &\approx& \frac{1}{2m+1} \qquad\qquad t \approx 0 \\ F_m(t) &\approx& \frac{(2m-1)!!}{2^{m+1}} \sqrt{\frac{\pi}{t^{2m+1}}} \qquad \qquad \textrm{large } t \end{eqnarray*}$

with the middle regime being interpolated via Taylor series or Chebyschev polynomials.

Accurate Calculation

For very precise computation of the Boys function (for example, for higher precision floating point, or for calculating the values for an interpolation grid), a practical (although slow) method is given derived from the formulation given by Shavitt.

The first step is to approximate the value of the Boys function via the large- $t$ approximation:

$F_m(t) \approx \frac{(2m-1)!!}{2^{m+1}} \sqrt{\frac{\pi}{t^{2m+1}}} \qquad \qquad \textrm{large } t$

Next, the error associated with this approximation can be estimated by the (finite!) sum

$\begin{eqnarray*} \Delta F_m(t) &\approx& \frac{e^{-t}}{2t} \sum_{i=1}^{[N]} a_i \\ a_0 &=& 1 \\ a_i &=& \frac{2m-2i+1}{2t}a_{i-1} \end{eqnarray*}$

making note of the fact that the summation starts at 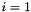$i=1$ . The summation continues until 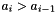$a_{i} > a_{i-1}$ , at which point the summation will continue to diverge.

Since it guaranteed that the true error is less than this value, it can then determined if the large- 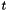$t$ approximation is acceptable. If it is not, then the small- 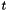$t$ (exact) formulation is used:

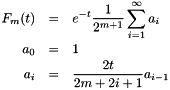
$\begin{eqnarray*} F_m(t) &=& e^{-t} \frac{1}{2^{m+1}} \sum_{i=1}^{\infty} a_i \\ a_0 &=& 1 \\ a_i &=& \frac{2t}{2m+2i+1}a_{i-1} \end{eqnarray*}$

again noting that the summation starts at 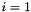$i=1$ .

The large- 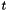$t$ approximation can be (conservatively) skipped if 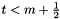$t < m+\frac{1}{2}$ , which also prevents a division by zero in the large- 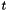$t$ approximation if $t=0$ .

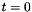By splitting the calculation this way, there are no pre-calculated thresholds (ie, between large- 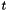$t$ and small- 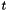$t$ formulae), which would necessarily depend on the value of 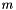$m$ and the desired precision of the calculation. The downside is that this procedure is quite slow.

In MIRP, the value of the highest value of 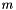$m$ is calculated in this fashion, and then downward recurrence is used to obtain the rest.

Functions in MIRP

In MIRP, the Boys function can be calculated via the following functions: